Jose Montero, PhD, WellCAD Product Manager
Rien Corstanje, Geologist & Hydrogeologist, Sales & Support Engineer

---

Fracture topology (from the Greek word tópos meaning “place, locality” and logy “study”) in the context of rock and reservoir analysis refers to the spatial relationships, connectivity, and structural arrangement of fractures within a rock mass. It focuses on how fractures intersect, form networks, and contribute to the overall flow paths for fluids, such as water, oil, or gas. Unlike basic fracture geometry, which describes individual fracture properties (like length, orientation, and aperture), fracture topology focuses on how these fractures connect to form complex networks that impact the permeability and structural integrity of the rock.

An example ilustrating how fracture topology can contribute to a better understanding of formation rocks can be seen in Figure 1. Here two fracture systems with an apparent similar fracture geometry and arrangement can be displayed. However, the topology is different. “A” shows a highly interconnected system whereas “B” includes isolated fractures. This arrangement will have significant implications for fluid mobility and distribution within each example.

Why Fracture Topology? How WellCAD can help?

In modern subsurface modeling, fracture topology—evaluated through fracture networks—has become a critical component for accurately assessing fluid flow, resource extraction potential, and structural integrity. This is because fracture networks are integral to evaluating the permeability, stability, and resource potential of rock formations. However, traditional fracture analysis’ methods often fall short in capturing the connectivity and spatial arrangement of fractures, which are critical for accurate subsurface simulations. WellCAD 5.8 introduces a powerful new fracture topology functionality, providing users with sophisticated tools to analyse fracture connectivity, network patterns, and flow pathways. This functionality not only enhances model precision but also offers a unique approach to visualising and quantifying complex fracture networks in rock masses.

Based on the work of Sanderson and Nixon (2015), the new Fracture Topology functionality developed for WellCAD 5.8 is set to redefine how geoscientists and engineers’ model and interpret fractured reservoirs.

How Fracture Topology works in WellCAD 5.8?

It is all about the nodes and branches.

In three dimensions, any fracture system consists of a series of finite surfaces or planes that either end at tip lines or intersect with other planes at branch lines. In two dimensions, these fracture surfaces intersect an observation plane (often an exposure surface or bedding plane) to create finite lines, known as fracture traces. These fracture traces will either terminate at their tips or intersect other traces. Isolated fracture traces may also occur (Figure 2).

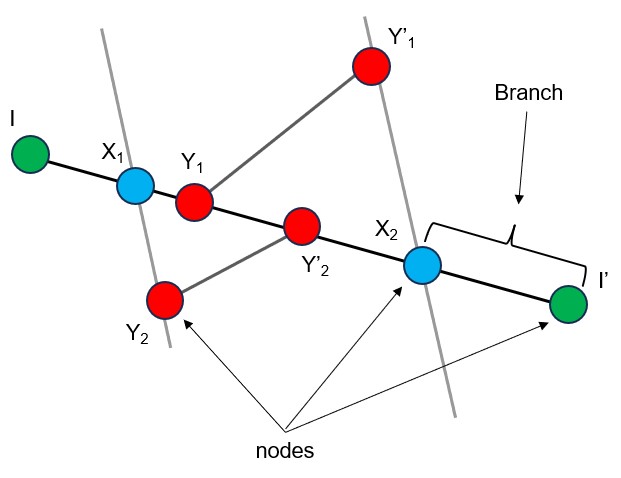
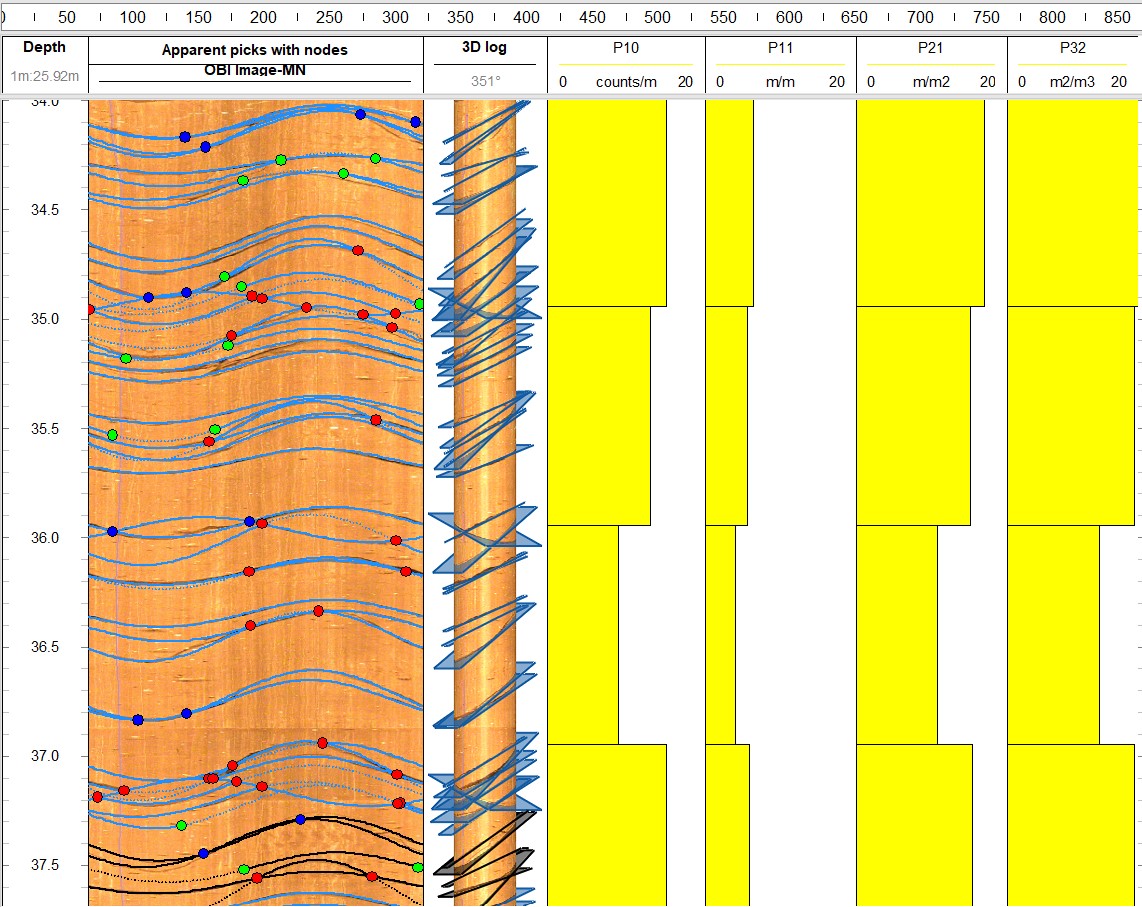
WellCAD 5.8 enables the interpretation of 2D fracture network’s topology as composed of lines, nodes, and branches, where each line has branches ending in nodes. Based on Manzocchi (2002), three node types are identified: isolated (I-green-nodes), intersecting fractures (X-blue-nodes), and terminating fractures (Y-red-nodes) (Figure 3).

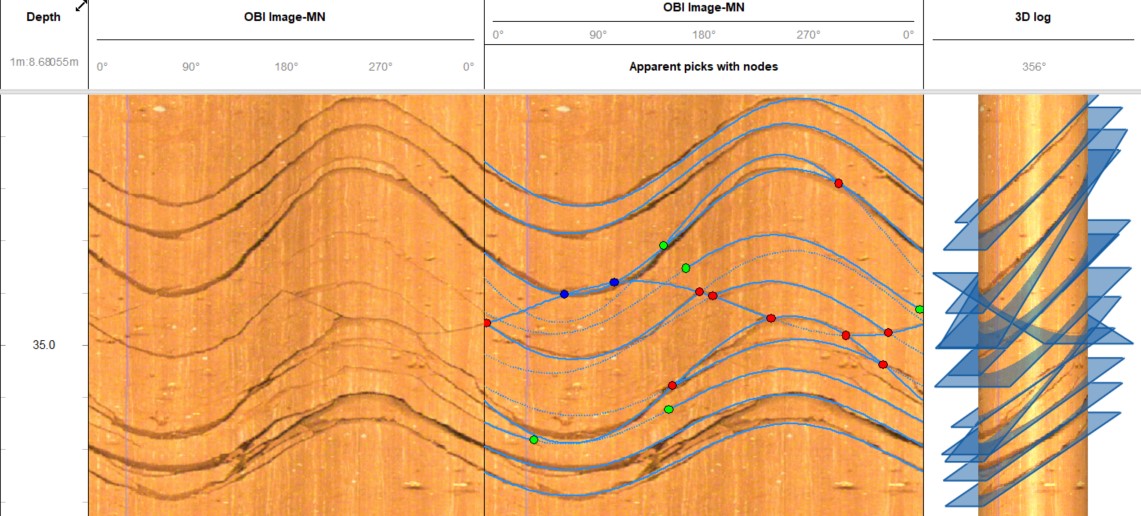
For the terminating (Y-red-nodes) and the isolated (I-green-nodes), a new partial picking functionality is implemented in WellCAD 5.8.

Advanced Insights with Fracture Topology Analytics in WellCAD 5.8

Once nodes are interpreted by the user and each fracture feature properly characterised (e.g., open fracture, closed fracture, open joint, etc) a process of node counting, and branch definition is enabled in WellCAD 5.8. This process can be enabled from the “Structure Interval Statistics” functionality that can be enhanced to deliver the following outputs: 1) Node Distribution, 2) Branch Distribution, 3) Branch Connectivity, 4) Line Connectivity and 5) Nb/Nl ratio.

These are 1D log outputs that inform from the type of fracture network a given dataset includes. One of the most important outputs is the Nb/Nl ratio used to characterize the fracture connectivity of a formation rock. The Nb term stands for the “number of branches” and the Nl to the number of interpreted lines. When the Nb/Nl ratio approximates to 1, the system is dominated by isolated features whereas ratios >1 will indicate a system dominated by cross-cutting features. When values tend to 2, the system may be poorly connected but if values are close to 10 or higher the system can be considered highly connected by fractures. Figure 4 illustrates the Nb/Nl ratio output in relation with the other types of 1D logs resulting from the fracture topology statistical analysis. Results indicate a poorly connected fracture system for the selected dataset.

Precision Ternary Plots in WellCAD 5.8

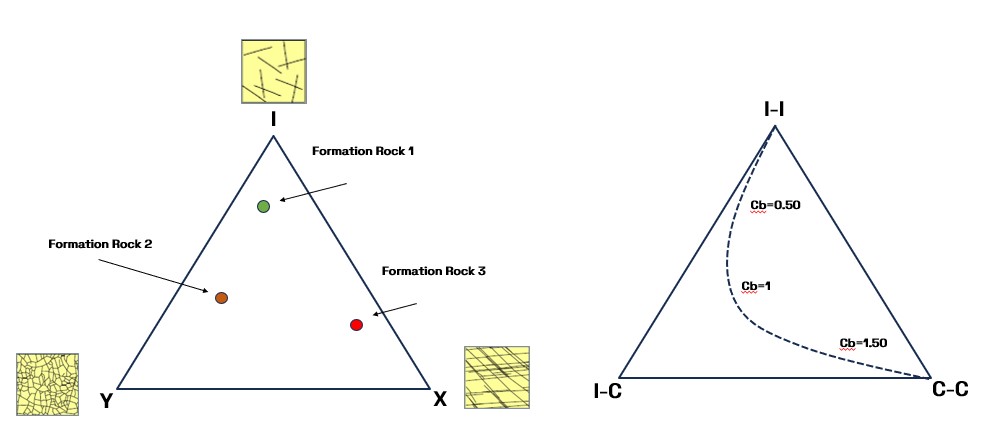
Ternary plots can also be displayed in WellCAD 5.8 to evaluate the fracture node distribution and fracture branch distribution of a given dataset. These are very valuable tools in fracture topology analysis because they effectively represent the proportional relationships and variability of key fracture attributes within a single plot. This is especially helpful when working with three main fracture characteristics that influence connectivity, fluid flow, and network structure. Both fracture node distribution and fracture branch distribution plots can be enabled as a type of Polar/rose plot in WellCAD.

The fracture node distribution ternary plot can be deployed alongside the previously shown 1D statistical logs for an intuitive visualisation of the proportions of three interdependent variables, such as fracture connectivity (I-nodes, Y-nodes, X-nodes), orientation, or size distributions. This helps in understanding the dominance of certain fracture types or attributes within a network. Figure 5 indicates the three main domains a formation rock may include but of course a mixed behaviour between the “I”, “Y” and “X” domain is always expected.

The fracture node distribution ternary plot can also be used for a comparison of Network Types existing in a formation rock. By plotting different fracture networks or simulations, one can observe how natural versus synthetic or random networks vary in their node distribution, providing clues about how natural processes versus random events shape fracture connectivity. Critical connectivity limits analysis can also be performed. Dashed lines (e.g., overlays for Nb/Nl ratio, Cl-line connectivity, Cb-branch connectivity) are added to indicate specific thresholds, such as the critical number of intersections required for a fully spanning, connected cluster within the network (Figure 6).

On the other hand, the fracture branch distribution ternary plot represents the proportions of different branch types that describe the segments between nodes. This plot allocates three different domains for “isolated branches” (I-I), “Cross-Cutting branches” (C-C) and “Dead-end branches” (I-C) (Figure 5). Key insights that can be extracted from this type of plot can be associated with 1) network complexity; Branch distribution indicates how complex the fracture network is in terms of potential flow paths and structural connectivity. Networks with a high proportion of connected branches are often more complex and have better fluid connectivity. 2) flow pathway Potential; understanding branch distribution helps in predicting flow paths, as higher proportions of connected branches suggest more pathways for fluid migration, whereas isolated and dead-end branches indicate barriers or restricted pathways. And 3) network comparison and stability; Similar to node distribution, comparing branch distributions across various networks can reveal how natural versus artificial networks differ in connectivity, helping to identify stable versus unstable regions in a fractured system.

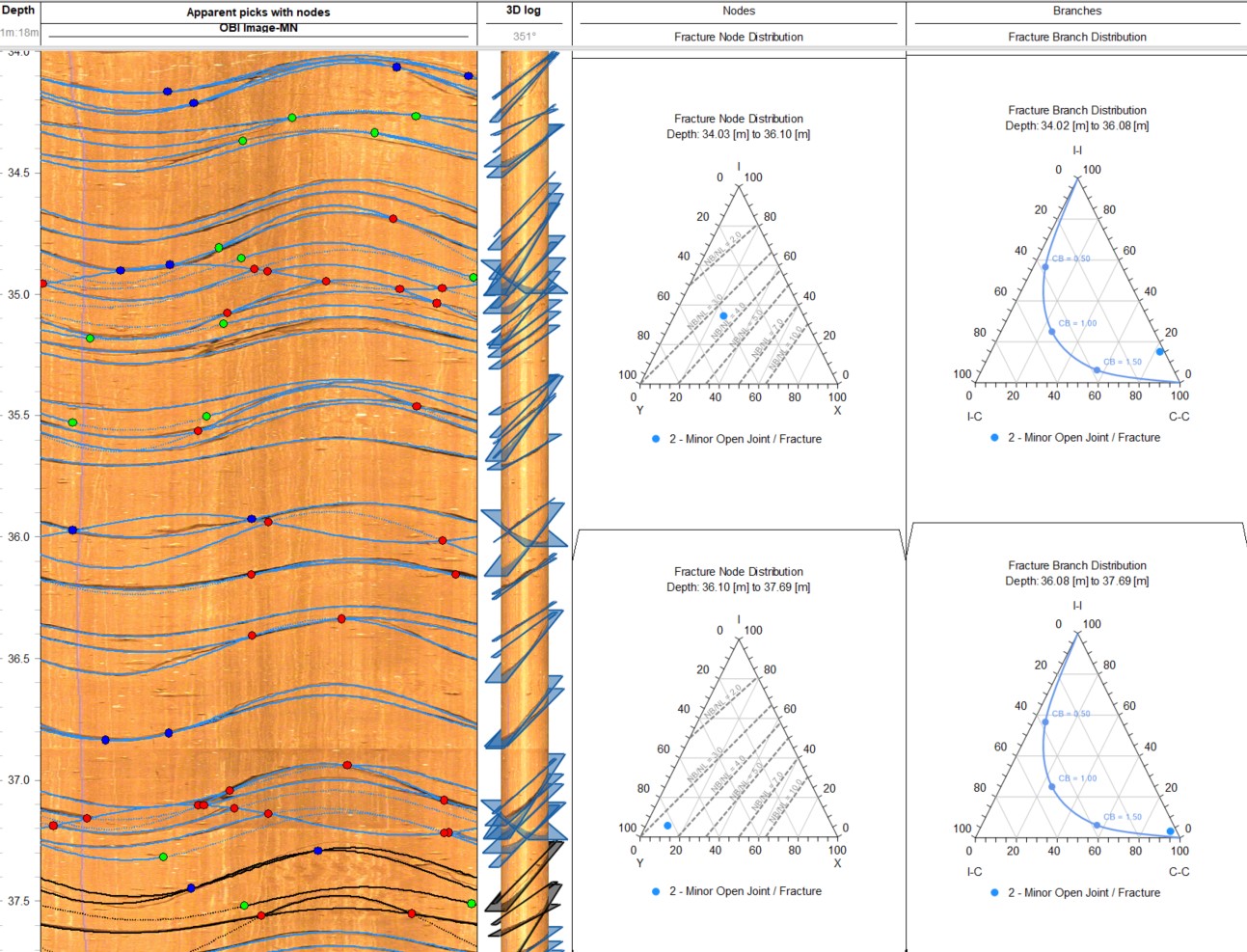
Ternary plots also promote the assessing and comparison of different fracture networks or segments of a network in a single ternary plot or in various plots associated to different depth intervals (Figure 6). This can reveal differences in fracture development or flow potential, which is particularly useful in geological reservoir studies applied to reservoir engineering, geothermal energy, and groundwater flow studies. Furthermore, ternary plots can be useful to identify trends, patterns, or outliers quickly.

Pxy Statistics in WellCAD 5.8

The Pxy statistics is a quantitative method used in fracture characterization to assess the distribution, density, and spatial arrangement of fractures within a rock mass. This statistical framework, often applied within the Discrete Fracture Network (DFN) modelling approach which needs from 1D log inputs to make it work (P₁₁, P₂₀, P₃₀, etc.). WellCAD 5.8 can now provide these outputs and offers a way to quantify and describe the topological aspects of fracture networks by focusing on intersections, endpoints, and connectivity patterns among fractures.

Defined by Sanderson and Nixon (2015), a fracture can be described by its dimension (Dimension of the feature) and the dimension of the sample region where that given fracture is enclaved (Figure 7).

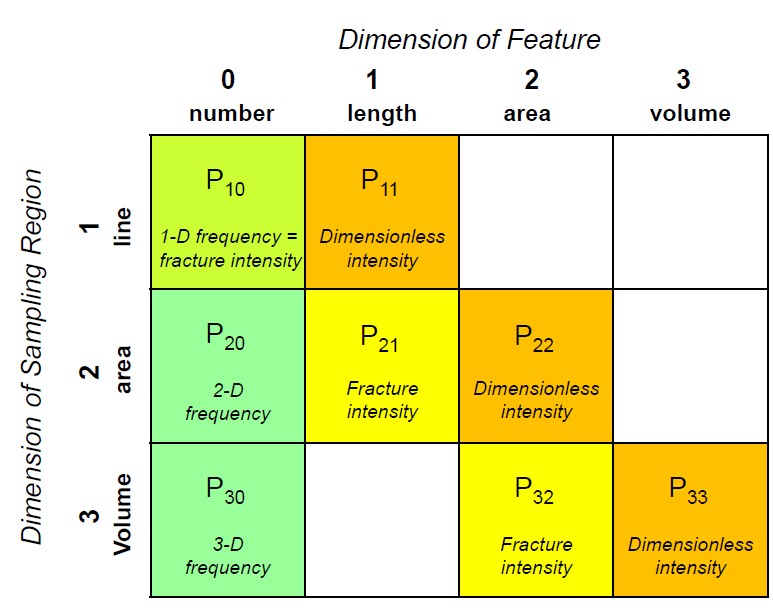
WellCAD 5.8 delivers the following P statistics (Figure 8):

P₁₀: The number of fractures per unit length of borehole (counts/m).

P₂₁: Fracture trace length per unit area.

P₃₂: Area of fractures per unit volume of rock.

P₁₁: Fracture trace length per unit length of borehole.

P₃₃: Volumetric fracture intensity or fracture density in 3D space

These components allow for a standardised assessment of the topological characteristics of a fracture network, providing a detailed picture of how fractures interact and the extent of their connectivity.

Fracture topology Applications: A game-changer in Fracture Analysis

Fracture topology analysis has versatile applications across various fields, particularly in understanding subsurface formations and optimising resource extraction. Key applications include:

• Hydrocarbon Exploration and Production: Fracture topology helps in predicting fluid flow paths in oil and gas reservoirs. By analysing fracture connectivity and node types, engineers can assess the reservoir’s permeability and identify optimal drilling locations to maximize recovery.
• Geothermal Energy: In geothermal systems, understanding fracture networks is crucial for determining heat and fluid pathways. Fracture topology analysis aids in assessing how connected the fractures are, helping to identify zones of high thermal conductivity and improve energy extraction.
• Groundwater Management: For groundwater aquifers, fracture topology aids in modelling flow patterns and recharge rates. It allows hydrogeologists to predict how fractures facilitate or restrict water movement, which is vital for sustainable groundwater extraction and pollution management.
• Mining and Quarrying: In mining, fracture topology is essential for evaluating ore body connectivity and assessing structural stability. Understanding fracture patterns helps in designing efficient excavation strategies while minimising risks of collapse or environmental impact.
• Carbon Capture and Storage (CCS): For CCS projects, fracture topology is used to assess the sealing capacity of geological formations. It helps in predicting whether stored CO₂ could migrate through fractures, aiding in the selection of secure injection sites for long-term carbon storage.
• Seismic Hazard Assessment: In regions prone to earthquakes, fracture topology contributes to understanding fault connectivity and stability. It helps geoscientists model how energy might be distributed through rock formations, which is essential for assessing seismic risk and guiding building codes.
• Civil Engineering and Infrastructure: In tunnel construction, dam building, and other civil engineering projects, fracture topology analysis informs stability assessments of the surrounding rock. It helps in identifying potential hazards related to rock fracturing and optimising designs to ensure structural safety.

These applications highlight the importance of fracture topology for both economic and environmental aspects, providing critical insights for safe and efficient subsurface operations.

References

Manzocchi, T., (2002). The connectivity of two-dimensional networks of spatially correlated fractures. Water Resour. Res. 38.
http://dx.doi.org/10.1029/2000WR000180.

Sanderson, D. J. and Nixon, C. W., (2015). The use of topology in fracture network characterization. Journal of Structural Geology, 72, 55-66.
https://doi.org/10.1016/j.jsg.2015.01.005